Fünf Platonische Körper
Um den kreisförmig angelegten Platz sind die Kantenmodelle der sogenannten „Fünf Platonische Körper“ gruppiert. Das sind Körper, die sich dadurch auszeichnen, dass sie von lauter regelmäßigen Vielecken begrenzt sind, dass sie konvex sind, und dass an jeder Körperecke jeweils gleichviel dieser Vielecke zusammentreffen. Der bekannteste Vertreter unter ihnen ist der Hexaeder oder Würfel.
Die Faszination, welche von diesen einzigartig schönen mathematischen Gebilden ausgeht, überdauerte Jahrtausende: Im XIII. Buch von Euklids berühmten „Elementen“ (um 300 v. Chr.) werden diese Körper konstruiert, und es wird gezeigt, dass es außer diesen fünf Körpern keine weiteren derart regelmäßigen Körper geben kann.
Benannt sind die Platonischen Körper nach dem griechischen Philosophen Platon ( ca. 428 – 348 v. Chr.). Für ihn war die Tatsache, dass es nur fünf dieser Körper geben kann, so bedeutend, dass er sie in seiner Lehre den vier antiken Elementen bzw. dem Kosmos zugeordnete: Tetraeder – Feuer, Würfel – Erde, Oktaeder – Luft, Ikosaeder – Wasser, Dodekaeder – Kosmos. Aus der Zeit der Megalith-Kulturen (4500-2000 v. Chr.) stammen gravierte Steinkugeln mit Polyedersymmetrie.
Der Schweizer Mathematiker Euler (1707 – 1783) entdeckte die Polyederformel, welche Ecken-, Kanten- und Flächenzahl nicht nur eines Platonischen Körpers, sondern eines beliebigen, konvexen, von ebenen Vielecken begrenzten Körpers miteinander verbindet. In der Mitte des 20. Jahrhunderts schuf der Architekt Buckminster Fuller riesige Kuppelbauten in Form „abgerundeter“ Ikosaeder, z. B. beim US-Pavillon auf der Weltausstellung Expo67 in Montreal.
Eine ebenso bemerkenswerte Tatsache ist, dass alle fünf Körperstrukturen in der belebten bzw. unbelebten Natur vorkommen, z. B. bei Kristallen, Plankton, Algen und Viren.
Fragestellungen und Aufgaben zu den Platonischen Körpern
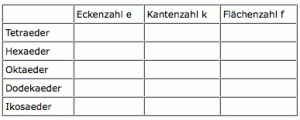
- Man begebe sich in den Mathematik-Garten und zähle für jeden der fünf Körper die Anzahlen der Ecken, Kanten und Flächen und trage diese in die folgende Tabelle ein.
Man finde eine, für jeden der fünf Körper gültige, Formel, welche die Ecken-, Kanten- und Flächenzahl miteinander verbindet. Bemerkung: e+k+f=5 ist z. B. eine Formel, welche Ecken-, Kanten- und Flächenzahl miteinander verbindet, jedoch nicht die Lösung dieses Problems darstellt.
- Warum kann es keinen Platonischen Körper aus lauter regelmäßigen 6-Ecken geben ?
- Welches ist wohl der „rundeste“ unter den fünf Körpern ?
- Wenn man den Würfel „abwickelt“ erhält man sein Netz. Wie viele solcher verschiedenen Netze gibt es insgesamt ? Bitte, setzen Sie die begonnene Reihe fort !
- Man gebe eine möglichst genaue Schätzung für das Volumen der einzelnen Körper im Mathematik-Garten.
>> Interessante Links zu diesem Thema
www.mathematik.ch/anwendungenmath/vorlagen/platon.php
www.fonline.de/home/fo0126/geometrie/geo57.htm